Roubo no Louvre: problema matemático com mais de 50 anos poderia ter impedido ação dos criminosos no museu

O cenário parece saído de um filme de ação: em plena luz do dia, um grupo de ladrões sobe em uma plataforma mecânica, corta a janela do primeiro andar do Louvre e, em apenas oito minutos, foge com oito joias napoleônicas de valor inestimável. O crime, que abalou a França e deixou o mundo perplexo, colocou sob os holofotes uma questão tão intrigante quanto preocupante: como o museu mais famoso do planeta foi roubado assim?

Sete suspeitos já foram presos, mas as perguntas sobre o sistema de segurança do Louvre continuam. Em audiência no Senado francês, a diretora Laurence des Cars admitiu falhas graves: a única câmera que cobria a varanda usada pelos ladrões estava virada para o lado errado, e um relatório preliminar apontou que um terço das salas do Pavilhão Denon — onde ocorreu o roubo — sequer tinha câmeras de vigilância. Cortes no orçamento e na equipe de segurança tornaram o museu vulnerável. “Precisamos olhar para todos os lugares” (via BBC), afirmou Des Cars, prometendo uma revisão completa da proteção do Louvre.

Mesmo com os alarmes funcionando, o roubo é o terceiro caso de alto perfil em museus franceses em apenas dois meses, o que levou o Ministério da Cultura a revisar os protocolos de segurança em todo o país. Mas o episódio também reacendeu o interesse por uma teoria matemática criada há meio século — e que, curiosamente, tenta resolver exatamente esse problema: como garantir que cada canto de um museu tenha a devida vigilância?

Sorria, você está sendo filmado (ou deveria estar)

Em 1973, o teórico húngaro Václav Chvátal formulou o chamado problema da galeria de arte (ou art gallery problem), que busca responder: qual é o número mínimo de guardas ou câmeras necessários para vigiar todo o interior de um museu?

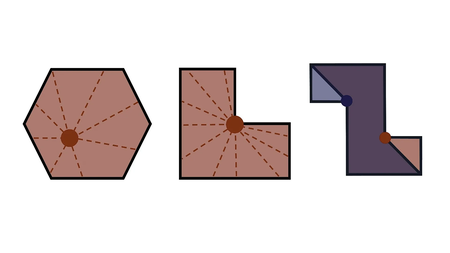As duas câmeras não são suficientes para a planta em forma de Z, enquanto uma é o suficiente para as outras duas.

A lógica é simples e tão genial que deveria, de fato, estar em museus. Imagine o mapa de um museu como um polígono, ou seja, uma figura formada por linhas retas e cantos. Cada câmera tem visão de 360 graus, e a missão é posicioná-las de forma que todo ponto da planta possa ser “visto” por pelo menos uma delas.

Para salas simples, como hexágonos ou retângulos, o problema é quase trivial: uma câmera pode dar conta de tudo. Mas conforme o formato se torna mais irregular — digamos, em forma de L ou Z — surgem áreas cegas, exigindo duas ou mais câmeras.

Chvátal descobriu uma fórmula geral: basta dividir o número de cantos (ou vértices) de uma planta por três para saber quantas câmeras são necessárias. Uma sala com 15 cantos, por exemplo, precisaria de cinco câmeras. Se o número não for divisível por três, arredonda-se para baixo — uma galeria com 20 vértices exigiria, no máximo, seis câmeras.

Anos depois, em 1978, o professor Steve Fisk, da Bowdoin College (EUA), ofereceu uma das soluções mais elegantes da matemática moderna. Ele provou que bastava dividir o espaço em triângulos e usar apenas três cores para marcar os vértices — vermelho, azul e amarelo, por exemplo. Escolhendo um único conjunto de vértices (digamos, os vermelhos), era possível garantir que câmeras nesses pontos cobririam todo o espaço.

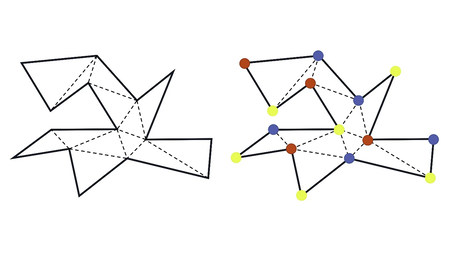É mais fácil saber onde posicionar câmeras após dividir a planta em triângulos e dar diferentes cores para cada câmera dessas áreas.

Na prática, isso significa que até galerias com formatos complexos poderiam ser vigiadas com um número mínimo de câmeras. Com a tecnologia atual, que inclui câmeras omnidirecionais e sensores inteligentes, a matemática de Chvátal e Fisk torna-se ainda mais eficiente e barata, o que é muito importante no mundo de hoje — com museus precisando cortar diversos custos.

Curiosamente, o Louvre parece ter ignorado uma versão dessa lógica: o “problema da fortaleza”, uma variação do teorema voltada para vigilância externa. Des Cars reconheceu que as câmeras do perímetro do museu “não cobrem todas as paredes”, o que permitiu que os ladrões se aproximassem sem serem detectados.

Em museus e além

A relevância do problema da galeria de arte vai muito além dos corredores de um museu. O mesmo raciocínio é aplicado em robótica, planejamento urbano, engenharia de comunicações e até inteligência artificial. Cidades usam o modelo para posicionar antenas de celular e sensores ambientais. Equipes de resgate aplicam o teorema para determinar onde colocar drones em áreas de desastre. Em palcos, ele ajuda a planejar a iluminação de modo que cada performer esteja sempre visível.

Na era da automação, o conceito também orienta sistemas de visão computacional e câmeras de carros autônomos — garantindo que nenhum “ponto cego” passe despercebido.

Enquanto isso, o Louvre tenta se recuperar do golpe, agora forçado a revisar sua infraestrutura e, quem sabe, olhar para a matemática com outros olhos. Afinal, com mais de 50 anos, fica bem claro que este problema matemático já devia estar nos museus.

Crédito de imagens: Jerome Gilles/NurPhoto via Getty Images, Kit Yates via BBC.